Occam's razor Archive Pages Categories Tags

Optimizing Merge Sort in Go: From Naive to Parallel

15 September 2023

I was practicing parallel merge sort for interview preparation and wanted to actually benchmark it to see the performance hit of a naive implementation. What started as a quick exercise turned into a rabbit hole of memory optimization, goroutine management, and some subtle bugs that took a while to figure out.

Along the way, I learned why the textbook implementation is deceptively inefficient, how to properly manage buffers to avoid unnecessary copies, and why my first two attempts at parallelization failed spectacularly (one was slow, the other deadlocked). Here’s what I found.

The Naive Implementation

Let’s start with the textbook version:

func MergeSortNaive(arr []int) []int {
    if len(arr) <= 1 {
        return arr
    }

    mid := len(arr) / 2
    left := MergeSortNaive(arr[:mid])
    right := MergeSortNaive(arr[mid:])

    return mergeNaive(left, right)
}

func mergeNaive(left, right []int) []int {
    result := make([]int, 0, len(left)+len(right))
    i, j := 0, 0

    for i < len(left) && j < len(right) {
        if left[i] <= right[j] {
            result = append(result, left[i])
            i++
        } else {
            result = append(result, right[j])
            j++
        }
    }

    result = append(result, left[i:]...)
    result = append(result, right[j:]...)
    return result
}

This implementation is clean and readable, but it has a problem: it allocates a new slice at every level of recursion. For an array of n elements, this means O(n) allocations, creating significant GC pressure.

Optimization 1: Pre-allocated Buffers

Instead of allocating at each level, we can allocate a single buffer upfront and reuse it throughout the sort:

func MergeSortSequential(arr []int) []int {
    if len(arr) <= 1 {
        return arr
    }

    buf := make([]int, len(arr))
    copy(buf, arr)

    return sequentialMergeSort(arr, buf)
}

But there’s a subtlety here. If we always merge from src into dst, we’d need to copy data back after each merge. The solution is to alternate buffers at each recursion level:

func sequentialMergeSort(src, dst []int) []int {
    if len(src) <= 1 {
        return src
    }

    mid := len(src) / 2

    // Recurse with swapped roles
    sequentialMergeSort(dst[:mid], src[:mid])
    sequentialMergeSort(dst[mid:], src[mid:])

    // Merge from dst back into src
    merge(dst[:mid], dst[mid:], src)
    return src
}

Why Alternating Buffers Work

At each level:

Children sort their portions and write results to their dst
Parent reads from those locations (now its src) and merges into its dst
No extra copies needed - data is always in the right place

Level 2: merge src → dst     (sorted data now in dst)
Level 1: merge dst → src     (reads from dst where sorted data is!)
Level 0: merge src → dst     (final result in dst)

Optimization 2: Parallelism

Merge sort is naturally parallelizable - the two recursive calls are independent. But naive parallelism has pitfalls.

Failed Attempt: Unlimited Goroutines

// DON'T DO THIS
go func() { left = MergeSort(arr[:mid]) }()
go func() { right = MergeSort(arr[mid:]) }()

This spawns 2^depth goroutines - exponential growth that overwhelms the scheduler.

Failed Attempt: Semaphore

// DON'T DO THIS EITHER
sem <- struct{}{}  // acquire
go func() {
    defer func() { <-sem }()  // release
    left = MergeSort(arr[:mid])
}()

This causes deadlock: parent goroutines hold semaphore slots while waiting for children that also need slots.

The Solution: Depth-Limited Parallelism

We only need log2(NumCPU) levels of parallelism to saturate all cores:

func MergeSort(arr []int) []int {
    buf := make([]int, len(arr))
    copy(buf, arr)

    // Calculate depth: log2(NumCPU) levels
    depth := 0
    for n := runtime.NumCPU(); n > 1; n /= 2 {
        depth++
    }

    return parallelMergeSort(arr, buf, depth)
}

func parallelMergeSort(src, dst []int, depth int) []int {
    if len(src) <= 1 {
        return src
    }

    mid := len(src) / 2

    if depth <= 0 {
        return sequentialMergeSort(src, dst)
    }

    var wg sync.WaitGroup
    wg.Add(1)

    // Spawn ONE goroutine, do other half in current goroutine
    go func() {
        defer wg.Done()
        parallelMergeSort(dst[:mid], src[:mid], depth-1)
    }()

    parallelMergeSort(dst[mid:], src[mid:], depth-1)
    wg.Wait()

    merge(dst[:mid], dst[mid:], src)
    return src
}

Key insights:

Only spawn one goroutine per level (not two) - current goroutine handles the other half
Depth limit prevents goroutine explosion
Still need to alternate buffers correctly

Benchmark Results

Testing on a 10th Gen Intel Core i5-10600K (12 threads):

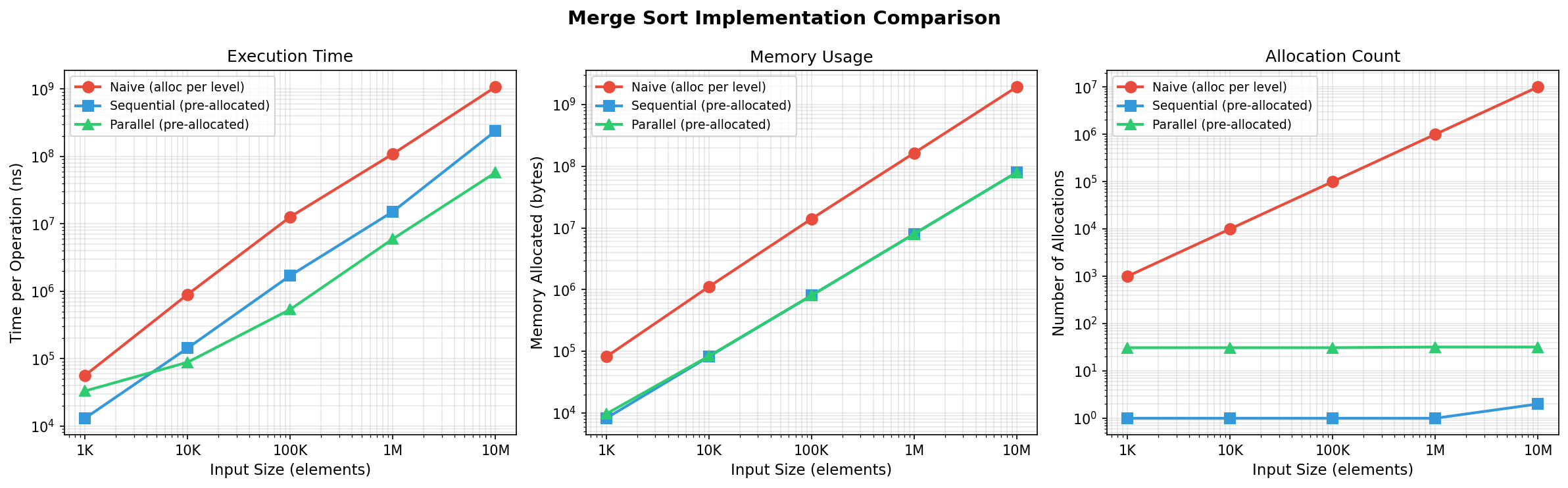
Benchmark Comparison

Execution Time

| Size | Naive | Sequential | Parallel |
|------|-------|------------|----------|
| 1K | 56µs | 13µs | 33µs |
| 10K | 895µs | 143µs | 88µs |
| 100K | 12.7ms | 1.7ms | 536µs |
| 1M | 109ms | 15.2ms | 6.0ms |
| 10M | 1.07s | 238ms | 58ms |

Memory Allocations

| Size | Naive | Sequential | Parallel |
|------|-------|------------|----------|
| 1K | 999 | 1 | 31 |
| 10K | 9,999 | 1 | 31 |
| 100K | 100,011 | 1 | 31 |
| 1M | 1,000,025 | 1 | 32 |
| 10M | 10,000,031 | 2 | 32 |

Speedup

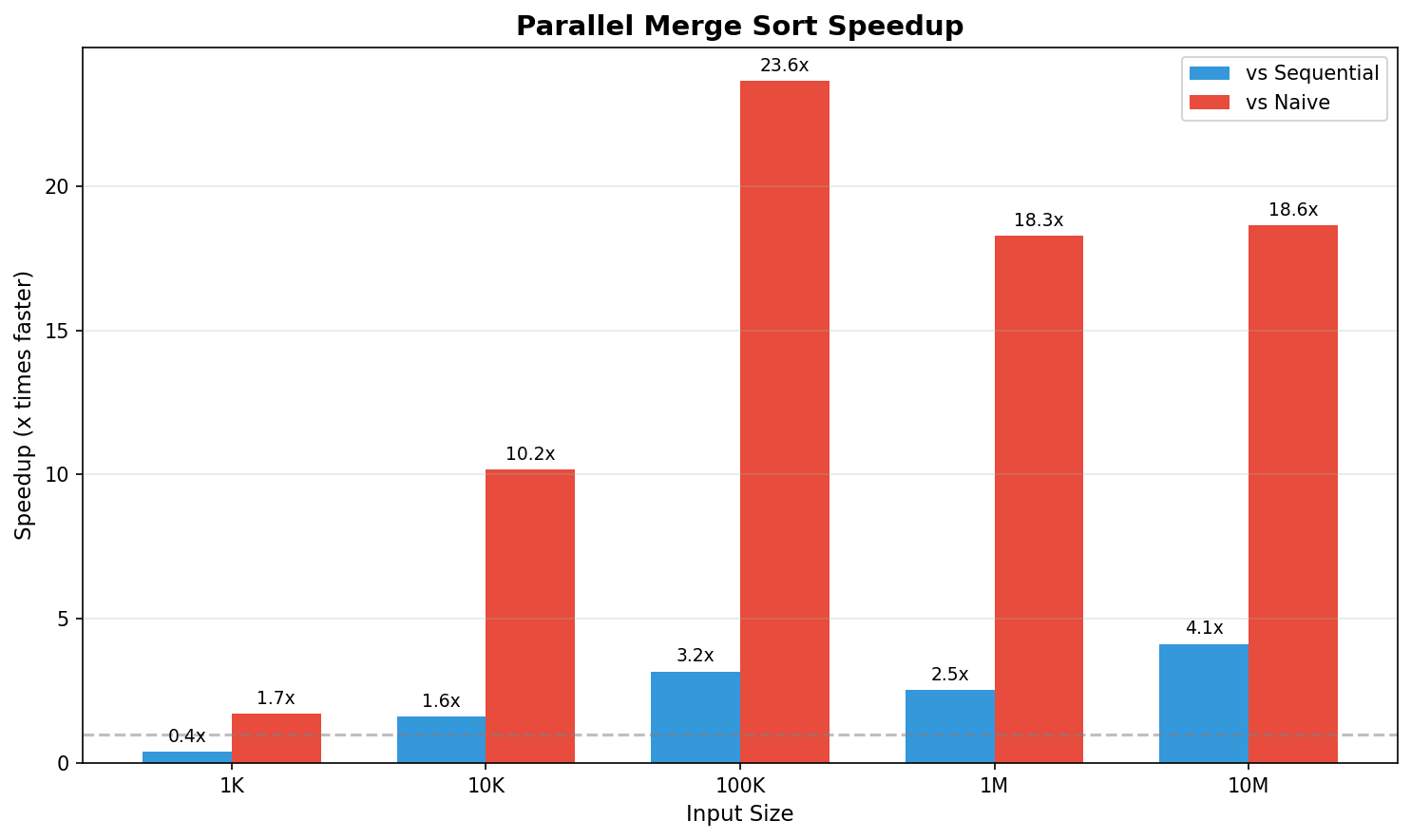
Speedup Chart

At 10M elements:

Parallel vs Sequential: 4.1x faster
Parallel vs Naive: 18.6x faster

Key Takeaways

Pre-allocation matters: Reducing allocations from O(n) to O(1) gives ~7x speedup even without parallelism.
Alternating buffers avoid copies: By swapping src/dst roles at each level, sorted data is always where the parent expects it.
Limit parallelism depth: You only need log2(NumCPU) levels of goroutines. More just adds overhead.
Spawn one goroutine, not two: The current goroutine can handle one half while a new goroutine handles the other.
Parallel overhead exists: For small inputs (1K), the sequential pre-allocated version is faster than parallel due to goroutine overhead.